Resonance: Journe, Breguet, And An "Odd Kind Of Sympathy"

"A riddle wrapped in a mystery inside of an enigma." – Winston Churchill

There are broadly speaking, two kinds of controversies in the community of watch enthusiasts.

First, there are differences in matters of taste – the size, placement, and presence or absence of date windows is a case in point. These controversies have very little if anything to do with actual functionality, and so, since they are largely a question of personal opinion, they provide endless fodder for everything from pleasant disagreement to deeply personal ad hominem attacks, and will probably continue to do so for as long as there are watch enthusiasts, and the means for them to publicly disagree with each other.

The second kind of controversy has to do with technical watchmaking and here, there are functional systems to discuss. The arguments are still, often, subjective to some degree but there is usually some grounding in actual physical systems and mechanical solutions. A classic example is the debate over whether or not the tourbillon offers any real practical advantage in a wristwatch. While the question is usually framed in such general terms that many of the actual disputes end up being apples to oranges comparisons (a single tourbillon, for instance, is not a multi-axis tourbillon and there are advantages and disadvantages specific to each) there are at least real-world mechanical systems at the heart of the debates.

Sometimes, though, there is so little actual data on the properties of a physical and technical system in watchmaking, that to all intents and purposes the argument becomes one of opinion anyway, and the question over what’s usually called “resonance” in watchmaking, is a case in point. So-called resonance watches are broadly speaking, those in which the two balances are somehow mechanically coupled, so that they begin to beat in synchrony with each other.

In Phase, Anti-Phase, And Resonance

The advantage to such systems is usually assumed to be, as clockmaker David Walter has said, that “Once they are set running and locked into anti-phase, each pendulum will correct errors in the other, should they occur.” Walter was speaking of pendulums but we can assume that the same advantage should be found in watches with two synchronized balances as well.

Before going any further, we should probably clarify what we mean by “resonance.” The term is commonly used for watches and clocks with two oscillators, set up so that they will beat synchronously. The phenomenon of oscillators influencing each other so that they begin to beat in time with each other can be observed in, for instance, metronomes set to the same tempo, which are placed on a mobile platform which transmits energy from one metronome to another. The effect is rather hypnotic to observe.

(Turned on to this video by @time2tic on Instagram).

As others have pointed out (e.g. Don Corson at WatchProSite; Justin Koullapis and Joshua Munchow at Quill & Pad) “resonance” in classical mechanics does not refer to coupled oscillators at all. (An aside: I can’t recommend Corson’s three part series on his software simulation of coupled oscillators highly enough). Instead, it refers to the increase in amplitude seen in an oscillator when it is driven by a force applied at or close to the oscillator’s natural amplitude. This is obviously related to the problem of coupled oscillators but the latter introduce considerable additional complexity and coupling two oscillators can produce unexpected and sometimes chaotic behavior.

A child’s swing is an intuitive example of resonance; you push the swing in time with its natural period and each swing will get larger and larger. A pendulum in a clock is another example; so is a balance in a watch. (A swing, of course, is a pendulum). If you push a swing at intervals that don’t correspond to its natural period, you get lower amplitude oscillations and you get a swing that oscillates irregularly and at low frequencies – you probably get an irritated kid as well.

What we’re actually talking about when we talk about so-called resonance clock and watches, are synchronized oscillators. For the purposes of a discussion of coupled oscillators in horology, we should clarify that an oscillator is any mechanism on which there is a driving force (the escapement) and a restoring force which ideally is proportional to the driving force.

Obviously without mechanical resonance such watches and clocks won’t work – each pendulum, or balance, wouldn’t be able to affect the other if they did not have roughly the same natural period – but the distinction is an important one because the physics of coupled oscillators has characteristics that a single resonant oscillator does not. That said I’m going to use the term “resonance” to refer to coupled oscillator watches and clocks, as it’s become the de facto term (after all F. P. Journe makes a Chronomètre à Résonance, not a Chronomètre à Oscillateur Synchronisé).

History, Huygens, And Getting Lucky

Before going any further, let’s look briefly at the experimental and technical history of resonance. The first person to observe synchronization of oscillators in mechanical timepieces was Christian Huygens, who invented the first pendulum clock. He was in this preceded at least conceptually by Galileo, who came up with a design for one, which was never completed. His son Vincenzo attempted to build a clock based on his father’s design but was unable to do so – perhaps partly because Galileo had by then gone blind and had to verbally describe his design rather than draw it; Vincenzo died before he could make a pendulum clock.

Huygens was a methodical person and kept detailed notes of his observations. These were read to the Royal Society in 1665, by Sir Robert Moray, with whom Huygens kept up a correspondence; the latter said in his remarks that Huygens had written about, “an odd kind of sympathy perceived by him in these watches [two maritime clocks] suspended by the side of each other.”

Huygens first noticed synchronization of two clock pendulums while observing (during a brief illness) two clocks, with pendulums of identical length, which were both mounted to a common support. He noticed that the two pendulums, once set going, would begin to oscillate in time, but 180º out of phase, over about a half an hour and if interrupted, would re-synchronize in anti phase again.

The two clocks in question were marine clocks, or at least an attempt at making a working marine clock – marine chronometers, in other words. This is relevant because the clocks both had quite massive weights hanging from them – these were meant to keep the clocks in a steady position on board a ship (rather like the gimbal systems used in boxed marine chronometers). The two clocks both used verge escapements and the pendulums swung, as verge pendulums must, through a fairly wide arc.

The weights weighed 100 pounds, and the mass ratio of each pendulum to the total mass of each clock and weight was 0.005. This is quite a dramatic discrepancy.

Science And Resonance

The reason that I mention the mass ratio is because it’s brought up as a critical parameter in a couple of the scientific papers that actually attempt to put synchronized pendulums on a solid mathematical foundation. Three fairly recent such papers are “On the problem of synchronization of identical dynamical systems: The Huygens’s clocks,” (Rui Dilão, 2008) the pithily named, “Huygen’s Clocks” (Bennett et. al. 2002) and more recently, “Huygens’ Clocks Revisited” (Willms et. al. 2017). Dilão cites 14 sources in his bibliography, including Bennett, of which the oldest that deals specifically with coupled pendulums is Kortweg, “Les Horloges Sympathiques de Huygens,” 1906. Willms cites 53 sources, although a number are primary sources including Huygens, as well as papers on coupled oscillator in other areas, including biological systems, and also papers on general numerical analysis of periodic behavior which were relevant to his group’s modeling.

Bennett & Co. noted that there were a couple of possible outcomes in their experiments. One was that the two pendulums in their apparatus would begin beating in sync, in anti-phase (that is, 180º out of phase, which is what Huygens observed) and the other a situation they called “beating death,” in which one pendulum would decrease in amplitude, and eventually stop when its amplitude was no longer large enough to unlock the escapement. The critical number here is the mass ratio – you mightn’t expect it intuitively but beating death only occurs in a situation where the mass ratio increases – that is to say, beating death actually occurs when the oscillators are more strongly coupled, and stable anti phase synchronization requires the oscillators to actually be more weakly coupled.

There are a number of videos online showing coupled pendulums, and the one above shows a typical result. The segment of string coupling the two pendulums, and the fact that almost all of the mass of the entire system is in the pendulum bobs, along with the fact that the pendulums are the same length, means that energy is periodically transferred completely from one pendulum to the other and one or the other pendulum will periodically stop completely.

Dilão, Bennett, and Willms all approach the problem as one of mathematical analysis – they created equations of motion for a coupled pendulum system and then checked to see whether or not the behavior observed in actual coupled pendulums matches the behavior predicted. In all cases the experimenters were successful (Dilão was able to model both in phase and anti phase synchronization) and in both cases, the onset of synchronization was shown to be highly sensitive to the initial conditions of the oscillators.

On Systems Behaving Non-Intuitively

The grossly oversimplified synopsis (which is all that I, non-physicist, and non-mathematician, am qualified to offer) is this:

Both mass ratio and the degree of damping in the coupling system between the two oscillators are critical in whether or not sustained anti phase oscillation occurs. Moreover, for any given combination of oscillator, coupling, amplitude, there are a number of different possible modes of synchronization and depending on your setup, and how closely the clocks match each other, you can observe in phase synchronization, anti phase synchronization, and other coupling phenomena as well.

These and other researchers all note that there was a hell of a lot of luck in Huygens’ observations. Willms for instance notes that under his analysis, only close adherence to the physical properties of Huygens’ system – in particular, the mass ratio between the pendulums and the overall system as well as the weak coupling of the oscillators – will produce anti phase synchronization, and that, “ … it was shown that substantial deviations away from Huygens’ physical set-up must be made in order for in-phase or other solutions to be stable.”

So, there are at this point some robust mathematical models for predicting whether or not two oscillators with similar frequencies will synchronize, and moreover, some predictable constraints on parameters in various physical systems for anti phase, stable synchronization to occur.

Breguet and Journe: Technical Solutions

The first resonance watches were as far as I know, created by Breguet, although as with the tourbillon it is unclear whether or not the idea of creating a resonance watch originated with him. Antide Janvier, however, is the first horologist known to have produced actual double pendulum resonance clocks. Three are known – one is in the Musée Paul-Dupuy in Toulouse; another is in the Patek Philippe Museum in Geneva, and as anyone who has visited his atelier will know, the third is in the headquarters of F. P. Journe, in Geneva. The only one of these which I have seen in person is the one at F. P. Journe.

The clock is an imposing structure. Like many long case clocks, it has an anthropomorphic feel and the movement, ticking away under glass, gives the impression of someone who has been buried alive.

The clock at the Journe manufacture was purchased by Mr. Journe at a 2001 auction for just north of $1.4M at a moment he described as “extremely emotional”. It currently lies within the company’s conference room alongside Journe’s watchmaking awards.

Breguet made three resonance watches that we know of. These are numbers 2667, 2788, and 2794. (Breguet also made two resonance clocks, numbers 3177 and 3671). The three resonance watches are very similar although there are some interesting differences as well, which you have to expect given the experimental nature of the watches.

Of the three, 2788 is probably the best publicly documented, since it was offered at auction by Sotheby’s in 2020, and the auction house provided a number of excellent images of both sides of the movement, as well as closeups of the balances:

Construction began in 1812 and the watch, sometimes called the “Prince Regent” as it was sold to the British Prince Regent who became George IV, was sold to its first owner in 1818. The two balances are both enclosed by shrouds intended to eliminate aerodynamic turbulence and interference, and the feet of each balance cock are just a few millimeters apart. The balance on the right, as well as some of the driving wheels, sit on a separate platform whose distance from the elements of the train, and balance, on the left, can be adjusted. There are on the right, also brightly polished steel cocks for the fourth wheel, escape wheel, and lever – there are corresponding cocks for the train on the left although since they are arranged differently they are slightly harder to spot. The two balances are impulsed by lever escapements.

This watch is part of the David Salomons Collection at the Meyer Museum Of Islamic Art.

As far as I can tell, no. 2667 and no. 2794 are constructed along the same general principles. However, no. 2667, which preceded no. 2788 and 2794, does have one interesting difference from the others. The two later watches both have balance cocks with feet directly adjacent to each other, while 2667, which appears to have preceded them, has balance cocks with the feet opposed to each other 180º.

Breguet no. 2794, photo from The Art Of Breguet, p. 2229, 3rd edition 1986, author George Daniels

Above is the movement of no. 2794. The balance on the right along with driving gears sits on a movable platform, like 2667 and 2788; unlike 2788, there are no shrouds around the balances to prevent aerodynamic turbulence. On the question of aerodynamic turbulence, Breguet went to some lengths to rule out air as a coupling medium. He wrote, as quoted by Daniels in The Art Of Breguet:

“ … the distance apart of the two circular balance systems can be varied easily to experiment with the influence of one upon the other, because I thought that the air would have a very great influence on their ability to work together. I was very surprised to find that it influenced the mechanism far less than the effort accorded each other by the impulsion of their mutual movements.”

Breguet no. 2667, image from Escapementmagazine.com

Of the three known Breguet resonance pocket watches which are known, only no. 2788 retains the anti-turbulence shrouds around the balances – as Daniels notes, Breuget, after testing the resonance system with the shrouds in place, as well as in a vacuum chamber, concluded that they were not necessary and therefore omitted them in no. 2794.

I don’t know of anything in Breguet’s own notes on why he changed the position of the balance cock feet from the opposed position in 2667, to the adjacent position in 2788 and 2794, but nothing he did was a coincidence and it seems reasonable to conjecture that he thought the coupling of forces between the two balances, would be better in the adjacent position.

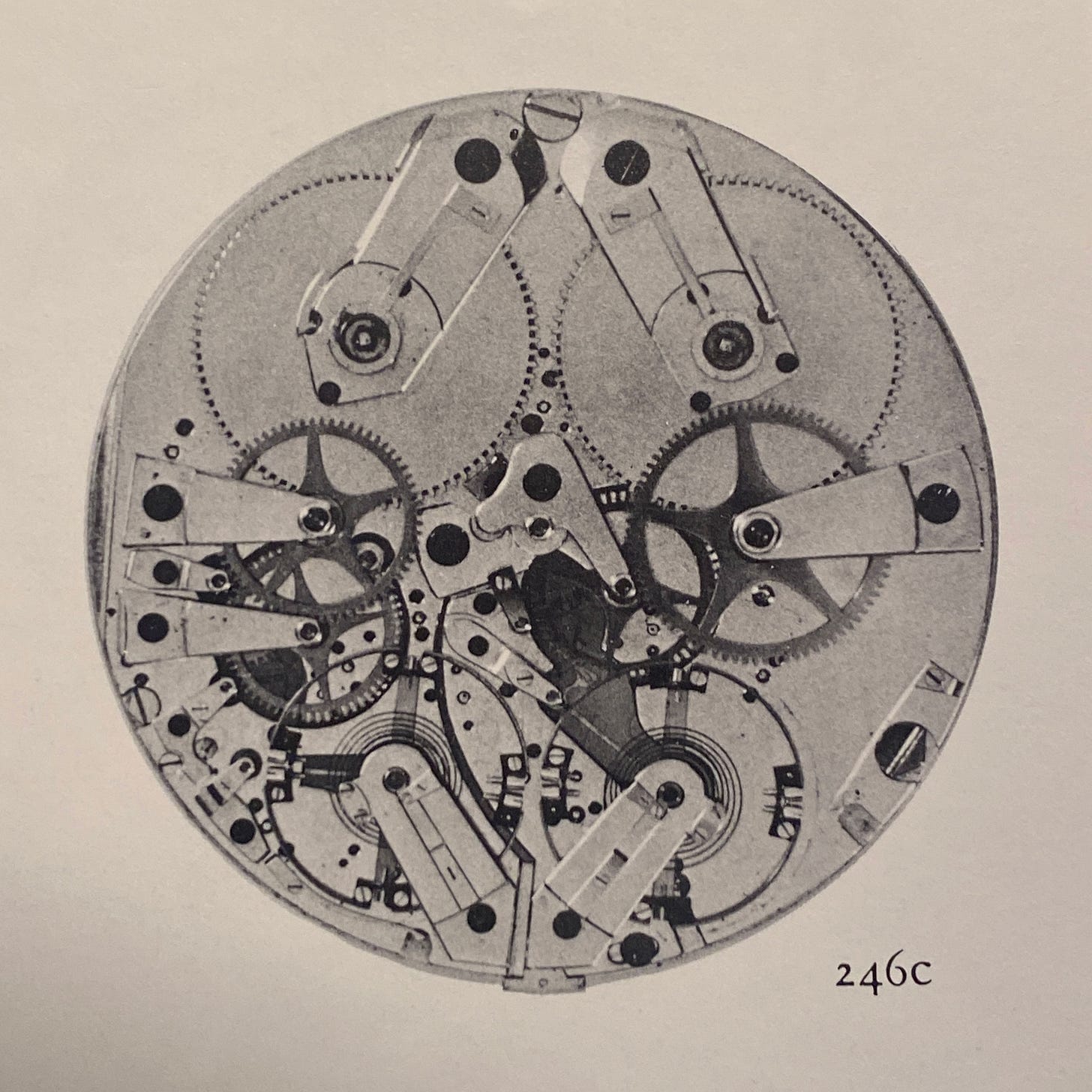
At this point, we can look at F. P. Journe’s technical solutions, in his first resonance movement, caliber 1499.3.

If you look along the edge of the movement you will see that it is pretty complicated in construction. There are three distinct layers to the caliber, as well as a system, as seen two hundred years before in Breguet’s pocket watches, for adjusting the proximity of the two balances to each other. The feet of the two balances are adjacent to each other as in the two latest Breguet resonance watches, numbers 2788 and 2794. The most noticeable difference is in the position of the feet of the balance cocks – in the latter two Breguets the feet are adjacent to each other and the outer edge of the movement plate, while in the Journe caliber, they are adjacent but with the feet almost at the center of the movement.

Does that matter? I don’t know. There was very little accidental about anything that Breguet did, and I doubt that Journe, who is perhaps the most assiduous student of Breguet’s work ever to come down the pike, changed Breguet’s arrangement at a whim either. Maybe it had to do with the challenge of fitting two trains into a wristwatch movement. Maybe he discovered, after his unsuccessful experiments with resonance in the 1980s, that position the cocks in this way gave a more robust coupling. Hey, I could ask him, but what fun is that?

In any case, the Journe resonance calibers are considerably more complicated in construction than you might expect (the newest version, caliber 1520, includes a differential in the gear train as well as a remontoire for each balance downstream from the differential. It’s an absurdly complex movement, and you have to wonder why Journe would go to all that trouble when the original Chronomètre à Résonance has been printing money for the last couple of decades. I think the updates make sense, though – the few Journe Resonance watches I’ve had a chance to experiment with, seem to show that resonance is most stable when balance amplitude and power reserve are strong. Once you get to the point in the power reserve where the remontoires don’t get enough power to rewind, coupling between the two balances seems to fall off.

Modern Coupled Oscillators

After looking at, as closely as possible, research that looks at how harmonic oscillators behave when they are mechanically coupled, there are a couple of things out of all the papers I’ve looked at which I think are worth noting.

The first, is that coupled oscillators do not necessarily behave the way you think they are going to. Huygens observed anti-phase coupling of pendulums under very specific circumstances. There was a specific mass ratio between the mass of the oscillators and the mass of the entire system and – and this is a key point – against what anyone would intuitively believe is true, you actually need very low mass in the oscillator and very high mass in the overall system, for what we call resonance – that is, coupling of two independent oscillators – to take place.

There is a lot of debate over what is or is not, “real” resonance and naturally, makers have a tendency to support the superiority of their own work. However, after reading as much as I think anyone ever has on the subject of resonance in horology, I feel that there are at least some, that are examples of deciding ahead of time based on the emotional appeal of one or another system, and then looking for reasons to justify the preference. This is not a sign of moral turpitude necessarily. But a thousand years ago, the Zen monk Dogen wrote, in his book Being-Time, that “man disposes himself, and construes this disposition as the world,” and so it is (if you ask me) with arguments over resonance.

So let’s start with the objection to F. P. Journe’s resonance watches that the forces involved are too weak for any coupling to occur across the movement plate. In fact, as we can see from Huygens’ own set-up, forces that are extremely weak can in fact produce a coupling of oscillators, (in anti phase, in the case of Huygens’ initial observations). So we can I think dispose of the argument that resonance is not occurring in F. P. Journe resonance watches, if the argument that it is not, is because the forces are too small and the coupling is too weak.

This is not to say that there are not differences between the systems. To some extent these are a matter of aesthetic preferences. Coupling two balances with a complex spring, as in the Armin Strom watches, somehow feels less pure to some purists but from a physics standpoint, the basic mechanics are the same; you have two oscillators, each with its own driving mechanism (the escapement) and its own restoring force (the balance springs) coupled with a secondary spring system. You can if you dislike this solution on aesthetic grounds, argue that what have are not two coupled oscillators, but rather, a single oscillator system with three springs exerting a restoring force (the two balances and the so-called resonance spring) but if you are intellectually honest you have to admit that the difference between such a system and a more traditional resonance system, a la Breguet or F. P. Journe, is in the details and not in the basic principles.

The Elephant In The Room

Now the elephant in the room, and maybe the joker in the deck too, is that of all the articles which describe the behavior of coupled mechanical oscillators, all take Huygens’ set up as the point of departure, which means that what’s being modeled in every case are the behaviors of pendulums. The big question then is, can these very sophisticated mathematical models apply to watches as well? Huygens had a set up with very specific properties – verge escapements, necessitating a large amplitude for relatively light pendulums and the serendipitous addition of massive stabilizing weights to each clock. You don’t need to exactly duplicate Huygens’ system to observe an anti phase mode of oscillation in a pendulum clock – Janvier, Breguet, and David Walter, to pick a modern maker, all deviated considerably from Huygens’ original configuration. But the question remains: do the mathematical models apply to a combination of balance spring, balance, and lever escapement?

What would be a very interesting next step, would be to take some modern resonance watches, and one of the mathematical models, and plug in some numbers from the watches. Amplitude, balance mass, and spring force are all known quantities (at least, to their manufacturers) and with those numbers in hand it ought to be possible to model synchronization modes as well as stability of the systems at different amplitudes.

Post-Script: The Moral Hazards Of Watch Writing

In thirty years of writing about watches I haven’t found a question more interesting than that of coupled oscillators and the truth is, it is a much bigger question than just one of horology.

Oscillators are everywhere. You can model almost any system of oscillators with an equation that includes a term for a spring couple – heck, I’ve found research modeling everything from a tennis volley to Aikido practice as a system of coupled oscillators. If there is any explanation for the perennial fascination that the subject of resonance seems to exert, maybe that’s it – we to understand resonance in miniature, because in doing so we intuit a connection to an infinitely larger world.

Further reading: Dr. Matt Strasser on “A Brief Tour Of Resonance,” a classical mechanics introduction to “A Ball On A Spring” and a look at the quantum mechanical ball on a spring. TL;dr, the quantum ball on a spring is quantized.