Solving The Perpetual Calendar Problem: A Modest Proposal

"We should take Bikini Bottom, and PUSH IT SOMEWHERE ELSE!" – Patrick Star, Spongebob Squarepants

Giant impact event; image, NASA

“That idea is just crazy enough … TO GET US ALL KILLED!” – Squidward Tentacles. (here is the clip if you aren’t a SpongeBob fan. I’ll wait. As you will see in the case of this Modest Proposal the objection is accurate).

Thanks partly to Audemars Piguet’s introduction of a perpetual calendar movement – the 7138 caliber – which has indications all of which can be set individually from the crown – and partly thanks to the introduction last year of the IWC Eternal Calendar, which has a moonphase with a precision of one days’ error every 45 million years, I have been thinking about the problem which calendar reforms like the Julian and Gregorian perpetual calendars are meant to solve.

The basic issue is well known to calendar mavens and to watch enthusiasts who are interested in perpetual calendar design: the length of tropical year, which is the year as reckoned by the length of time it takes for the Sun to cross a particular point on the celestial sphere, in much the same way that the solar day is reckoned by the return of the Sun to a given position in the sky during one rotation of the Earth on its axis. Like the solar day, the point you choose for the Sun’s return to a particular point in the sky for the tropical year can be arbitrary as long as you are consistent. One convenient point is the time it takes for the Sun to travel from one Vernal (Spring) Equinox to the next, which in 2000 was 365.24217 mean solar days (in the sky, this is the moment when the Sun in its path crosses the celestial equator).

From a calendar perspective you can see the problem. Calendars break up the year into whole numbers of days, so if you have a 365 day year in your calendar, you will have a leftover of slightly less than a quarter of a day, which means that your calendar will gradually drift out of synchronization with the actual year, and therefore with the seasons. The Julian calendar attempted to solve this problem by adding an extra day to February every four years, but this was also not an adequate correction and the Gregorian calendar added some additional rules – first, that every 100 years, you would omit the 29th of February, and once every 400 years, you add the 29th of February back in, as the 100 year rule still leaves an error. Perfectionists among us as well as the mathematically inclined will now note that the four year, 100 year, and 400 year rules are not perfect either, since this still leaves us with an error of 26 seconds per year, and the upshot of this is that about the year 4909, the Gregorian calendar will have accumulated a full days’ error. Since the Gregorian calendar was implemented in 1582, and 4909-1582 = 3327, we can conclude that it accumulates an error of one day every 3327 years, which is as close as never mind to the figure given by some authorities such as NASA .

We would like as perfectionists in the world of calendar reform, as well as watch enthusiasts, to do better than that, and of course some pretty smart folks have given thought to further corrections to the Gregorian calendar to prevent a days’ error every three millennia and change. In 1964 the presumably eminent Professor E. R. Hope, wrote in the presumably august Journal Of The Royal Astronomical Society Of Canada, in the article, “Further Adjustments Of The Gregorian Calendar Year” that:

“The astronomer Delambre in 1814 suggested that a further correction of the Gregorian calendar be made by omitting the leap-year day from A.D. 3600, A.D. 7200, A.D. 10,800, and so forth. The proposal nowadays most favoured (at least, we assume it to be the most favoured, since it is the only one now mentioned in the Encyclopaedia Britannica) is to omit the bissextile day in A.D. 4000 and at intervals of 4,000 years thereafter. This is more in the spirit of the Julian and Gregorian calendars, with their intercalation rules based on division by four and four hundred. It is stated that the residual error in the Gregorian calendar, when corrected each 4,000 years as above, will not exceed one day in 20,000 years. But this almost certainly is not true. It would be true if the present error accumulation rate (~3 days/10,000 years) were constant, which is not what has been observed. In fact, the suggested correction would achieve very little, aside from an extra complication in the calendar. It is surprising that no-one (so far as we are aware) has thought this matter through. It is not so remote a problem as may seem: indeed it faces us with at least one decision that is pressing hard upon us.”

“Pressing hard upon us” in this case means as Mr. Hope points out, that the Gregorian calendar fails to take into account that the mean solar or tropical year gets very slightly shorter every century by about 530 milliseconds. The failure of the Gregorian calendar to take this into account, he says, means that by 10,000 AD, the Gregorian calendar will have drifted out of synchronization with the solar year by five days and by 40,000 AD, by 56.5 days … the horror, the horror. Clearly, we can’t have this and he said (again, in 1964) that:

“This drift is not removed by omitting a bissextus each 4,000 years. If we desired to remove it by equally spaced adjustments over the 10,000 years, then the first adjustment is due in A.D. 2000-only 36 years from now.”

I believe we have missed the boat on this correction, although I have not gone so far as to contact, say, the US Naval Observatory, who are custodians of our time standard atomic clocks, to ask what they make of all this. The article from Mr. Hope points out, I think, the really insurmountable problem, which is that no matter how many corrections you add to the Gregorian rules, you are never going to achieve anything better than an approximation. A better solution, it seems to me, would be to simply move the Earth slightly in its orbit in order to modify the tropical year so that it is a whole number of days. To do so would involve slightly increasing the length of the year, or slightly decreasing it, and the only way to do this physically is to increase or decrease the size of the Earth’s orbit around the Sun, which can be done by very slightly increasing or decreasing the Earth’s orbital velocity.

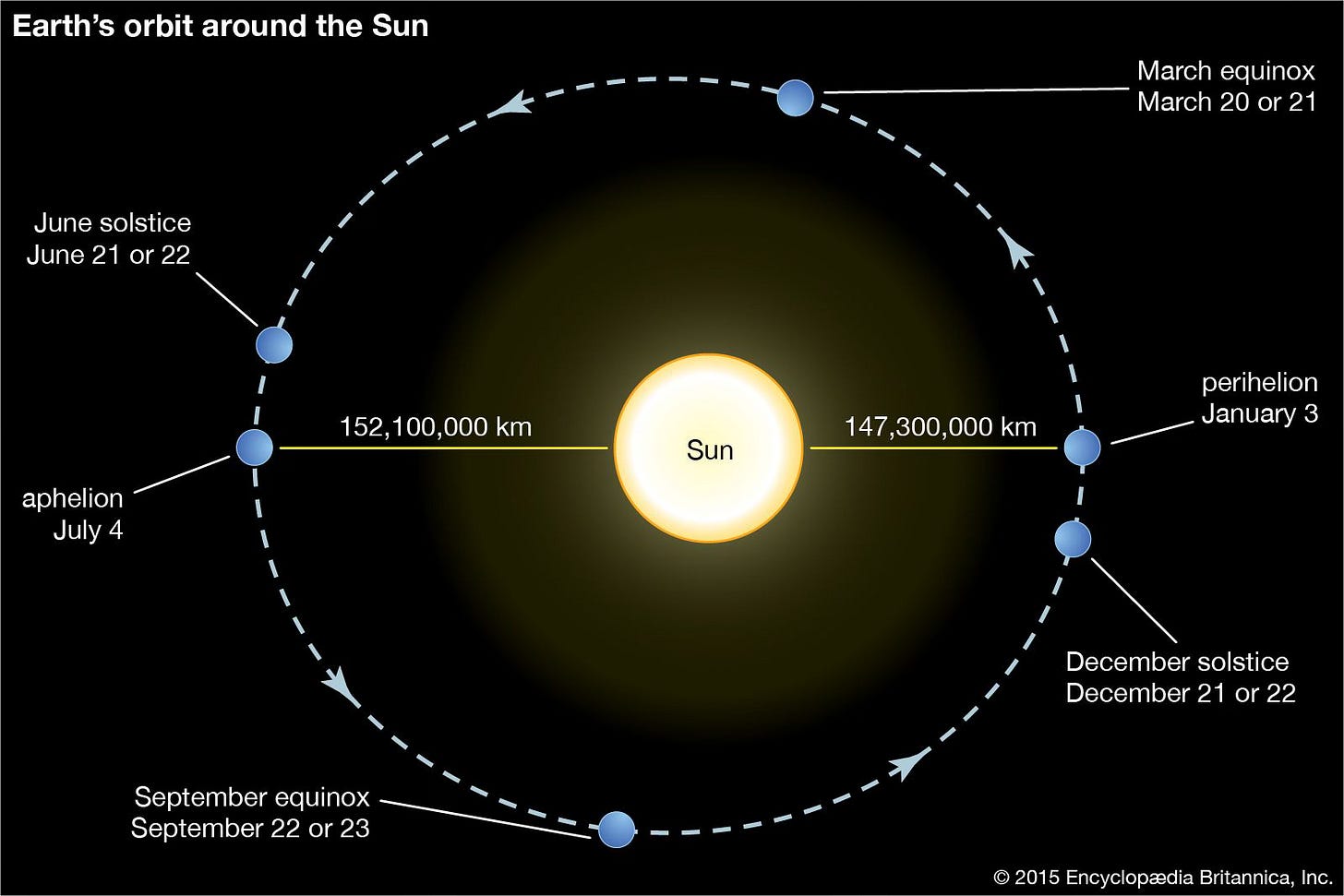
The Earth’s orbit is not a perfect circle; in fact it is elliptical, although only slightly. The eccentricity of the Earth’s orbit is about 0.0167, which means that at aphelion (the point at which the Earth is furthest from the Sun) the Earth is only about 3% further away than perihelion (the point at which the Earth is nearest to the Sun). The Sun sits at one of the two foci of this nearly circular ellips and the semimajor axis of the orbit, is the distance from the Sun to the Earth at aphelion. According to Kepler’s Third Law, the orbital period of a planet has a specific ratio to the semimajor axis of its orbit; the smaller the semimajor axis is, the shorter the orbital period. Therefore, increasing or decreasing the orbital period of the Earth can be viewed as a change in the length of the semimajor axis, which in turn requires a noodge to the Earth’s orbital velocity.

Source, appropriately enough, is the online Encyclopedia Brittanica

The increase or decrease in the length of the semimajor axis need only be enough to either increase the length of the year to 366 days or reduce it to 365. Having found ChatGPT useful for another hypothetical astrophysical calculation (“A Couple Of Watch Guys Sitting Around Trying To Figure Out How To Destroy The Solar System”) I turned to it (them?) again to find out how much the orbital velocity of the Earth would have to change, to bump a year up to 366 days or down to 365 days. The answer is that it wouldn’t take much of a change at all, or it doesn’t look like all that much. The current orbital velocity of the Earth is about 29.78 kilometers per second, and to get the year up to 366 days, you would need to increase orbital velocity to 29.86 km/s; to get it down to 365, you would need to decrease the orbital velocity to 29.70 km/s. The increase or decrease is small or at least it looks that way – a change of about 80 m/s would do it.

This becomes, to put it mildly, an engineering problem. The Earth has a mass of 5.972 × 10^24 kg. Generally speaking we (humans) are not especially good at understanding such large numbers intuitively although it helps to remember that in scientific notation, the number of the exponent (24 in this case) represents a shift of the decimal point one place to the right; the number is equal to 5,972,000,000,000,000,000,000,000 and of course, every additional zero means a tenfold increase in magnitude. The energy required for the desired alteration in orbital velocity and therefore, orbital period, is according to ChatGPT, immense to say the least; about 100,000 times the energy of the Chixculub impactor, which was responsible for the extinction event at the end of the Cretaceous which led to the extinction of all non-avian dinosaurs. This would leave us with a calendar that required no intercalary days for a 365 or 366 day year but no one would be around to appreciate the added convenience. You could of course, spread out the energy expenditure over hundreds or thousands of years – one way would be by towing an asteroid of sufficient mass into position near the Earth and using it as a gravity tractor.

This however would in turn, only prove to be a temporary solution as the Earth’s orbital period is not entirely stable anyway. The Earth is moving very slowly away from the Sun every year – not much; about 1.5 centimeters per year, but it is moving. Once the Earth has moved an additional 14,060,000,000 centimeters away from the Sun along its semimajor axis (amazing what you can do with computers these days, it’s not all ripping off Ghibli Studios) you’ll have a 366 day year, temporarily at least. (This is distinct from the accumulating error in the shortening of the tropical year, noted by the long aforementioned Mr. E.R. Hope, which is due to the precession of the Earth’s axis and therefore, the precession of the Equinoxes). At 1.5 cm/year, assuming a constant drift, it would take … ah, 9,373,333,333 years, at which point as you might expect, other issues …

The Earth in 5-7 billion years, as the Sun becomes a red giant

… will have made waiting out the extra fraction of a day at the end of a tropical year, even less practical than crashing 100,000 Chixculub impactors into your favorite Pale Blue Dot.

Perhaps therefore it is just as well to be philosophically resigned to approximations since we don’t have much of a choice anyway. Another option is to simply not care if the calendar drifts; the ancient Egyptians for instance don’t seem to have been very much bothered by it. In the 2012 book, Calendars In Antiquity, Sacha Stern writes, “Inasmuch as the drift of the civil calendar appears not to have been cause for concern or complaint in ancient Egyptian society, there is no need to search for the existence of an alternative, Sothic calendar” (the Sothic cycle being the period of 1460 years it would take for the drifting ancient Egyptian calendar to resynchronize with the seasons). What we really want is simply for our calendars to make sense in human terms and over the scale of human lifetimes, so the fact that there is not and never will be any such thing as calendar reform that can take into account all the infinite variations in the Earth’s orbital dynamics, need not trouble us. And anyway, most “Gregorian” perpetual calendars aren’t even Gregorian; they don’t take into account the 100 and 400 year rules which are the real distinction between the Julian and Gregorian calendars. As long as Halloween still comes, here in the Northern Hemisphere, when a chill is in the air and the days are shortening, for as long as I live my allotted threescore years and ten, I’m happy to call it … well, a day. And to really press home the point that the whole enterprise of calendar reform is pointless, there are things like the fact that none of this takes into account the changes in the Standard International Second, the effects of tidal lunar forces on the Earth’s rotation and precession of its orbit, the fact that beyond a certain point, everybody hates calendar reform, or even the fact that the length of the day is changing. Abandon hope, all ye who enter here.